1.概念
①什么是二叉树？
每个节点最多只有2个子节点的树，这两个节点分别是左子节点和右子节点。

②什么是满二叉树？
有一种二叉树，除了叶子节点外，每个节点都有左右两个子节点，这种二叉树叫做满二叉树。
③什么是完全二叉树？
有一种二叉树，叶子节点都在最底下两层，最后一层叶子节都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫做完全二叉树。

第一个是普通的二叉树，第二个是满二叉树，第三个是完全二叉树

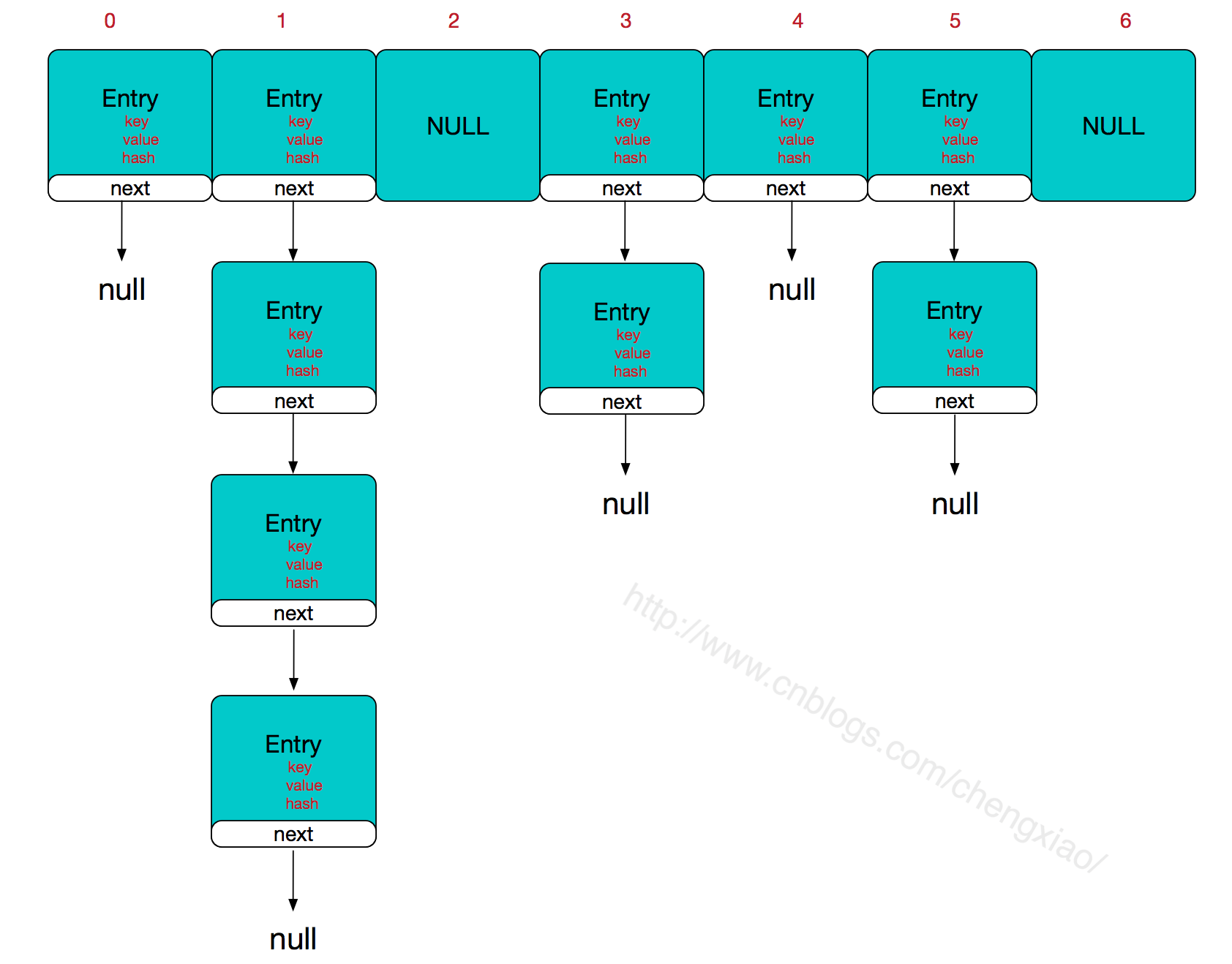
2.完全二叉树的存储
①链式存储
每个节点由3个字段，其中一个存储数据，另外两个是指向左右子节点的指针。我们只要拎住根节点，就可以通过左右子节点的指针，把整棵树都串起来。这种存储方式比较常用，大部分二叉树代码都是通过这种方式实现的。

②顺序存储
用数组来存储，对于完全二叉树，如果节点X存储在数组中的下标为i，那么它的左子节点的存储下标为2*i，右子节点的下标为2*i+1，反过来，下标i/2位置存储的就是该节点的父节点。注意，根节点存储在下标为1的位置。完全二叉树用数组来存储时最省内存的方式

不过，我刚刚举的例子是一棵完全二叉树，所以仅仅“浪费”了一个下标为 0 的存储位置。如果是非完全二叉树，其实会浪费比较多的数组存储空间。你可以看我举的下面这个例子。

因为非完全二叉树节点可能没有左子树或者右子树,如果该二叉树为一个单臂树那么浪费的空间便非常明显,当一棵树是完全二叉树或者是满二叉树时可以用数组存储时非常节省空间而且计算节点位置也非常方便 如果是非完全二叉树或者是单臂树时最好使用链表来存储。

（1）非空二叉树上的叶子结点数等于度等于2的结点数加1，即

大致的证明思路就是一个数的总结点数等于各个度的结点相加，然后也等于总边数加一。最后解出来。

（2）非空二叉树上的第i层至多有2^(i-1)个结点(i >= 1)

第一层至多有一个根结点，第二层至多有2个结点，依次类推，可以证明其为一个公比为2的等比数列。

(3)高度为h的二叉树至多有个结点

利用性质2求前n项和，即等比数列结果。

(1)具有n个(n > 0)结点的完全二叉树的高度为